BigEd wrote:
I started a
thread the other day to compare the two micros, but the best comparison would always be to code a solution to the same problem on both, using the best techniques in each case - which is a tall order!
That is exactly what I tried to do. And it took a lot of time. The 6800 is stupid simple. The 6502, with it's 8-bit indexes, a relatively vast array of addressing modes, and page crossing penalties, took a lot longer than expected. I still think I could get a bit more out of the 6502. Not so sure about the 6800.
To maximize the 6800 performance I had to use both accumulators as much as possible. The changeable stack pointer comes in handy for loading and storing 16-bit pointers. To do block moves without "indirect indexed" (i.e (foo),y) is a real pain with the 6800. However I was able to cheat by having one pointer use reg x and the other use the stack pointer. Then a simple block move looks like:
Code:
pula ;auto increments!
staa ,x
inx
Every example 6800 program I looked at had reg x being reassigned for each block, back and forth. That would kill performance. Esp. with long loops.
BigEd wrote:
Of course, different types of problem could well produce widely varying results, as the respective strengths and weaknesses play out.
Yep. Here is the profile of the 6502 code:
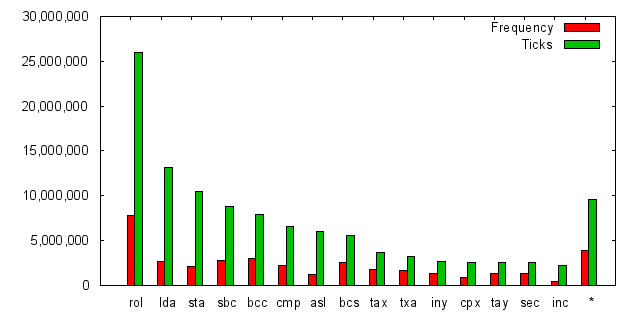
The 6800 and just about any other 8-bit processor without a hard div or mult would look the same. ROL dominates and many of the top 15 are used for division routines. The 6800 with its dual accumulators helped with optimization. (Notice the lack of BNE? Lots of unrolling :-).
BigEd wrote:
What do you think is behind Glen's time of 3:14? That he stopped optimising at that point? A complete coincidence??
Complete coincidence. Glen's code prompts for number of digits. I entered 1000 and timed it by recording the screen output. 3:14. Awesome.
BigEd wrote:
(Does it make any sense to wonder about base 100? Or is that in effect what Glen does, maybe using BCD mode?)
Go for it! I am not interested, since BCD math on any 8-bit processor is not as complete as binary math.







